1. 다익스트라 shortest-path 알고리즘이 있다. line 9와 line 10에서

1 Initialization:

❖ c(i,j): link cost from node i to j; infinite cost for indirect neighbors; ≥0 ❖ D(v): current value of cost of path from source to destination v ❖ p(v): previous node (neighbor of v) along path from source to v ❖ N’: subset of nodes; v is in N’ is least cost path (or min D(v)) from source to v definitively known ▪ Initiallyonlysourcenode(u)

N’ = {u};
for all nodes v
if v adjacent to u then D(v) = c(u,v);
else D(v)= ∞ ;
Loop
find w not in N’ such that D(w) is a minimum; add w to N’;
update D(v) for all v adjacent to w and not in N’ :
     if D(w) + c(w,v) < D(v) then // w gives us a shorter path to v than we’ve found so far
until N’=N;

2. LS 와 DV 알고리즘을 비교하세요.

## Link State

• global 모든 라우터의 정보를 가지고 있다. Adjacent link cost를 모든 라우터에게 방송 한다. 즉, 라우터는 전체 네트워크의 사진을 얻게 됨. 라우터는 전체 네트워크에의 link cost 정보를 받고 각자 독립적으로 최단 거리를 구한다. (Dijkstra’s algorithm)

Dijsktra’s Algorithm

Input : Network topology, link cost Output : 한 노드에서 다른 노드를 향할 때 최단거리 가 작성된 forwarding table

## Distance Vector

• decentralized 라우터는 물리적 연결 되어 있는 이웃과 그 코스트를 알고 있다. 반복적인 계산, 이웃간의 정보 교환이 이루어짐. Adjacent link cost를 이웃 라우터와만 교환 한다. 각각의 라우터는 넥스트 홉의 최단 거리를 계산한다. (BellmanFord Algorithm)

3. 아래 네트워크에서 EA의 링크 코스트가 3에서 40으로 바뀌었다. count-to-finity 문제와 해결책인 poisoned reverse 를 DV 알고리즘으로 설명하세요. node E와 D가 목적지 A를 향한다고 가정합니다.

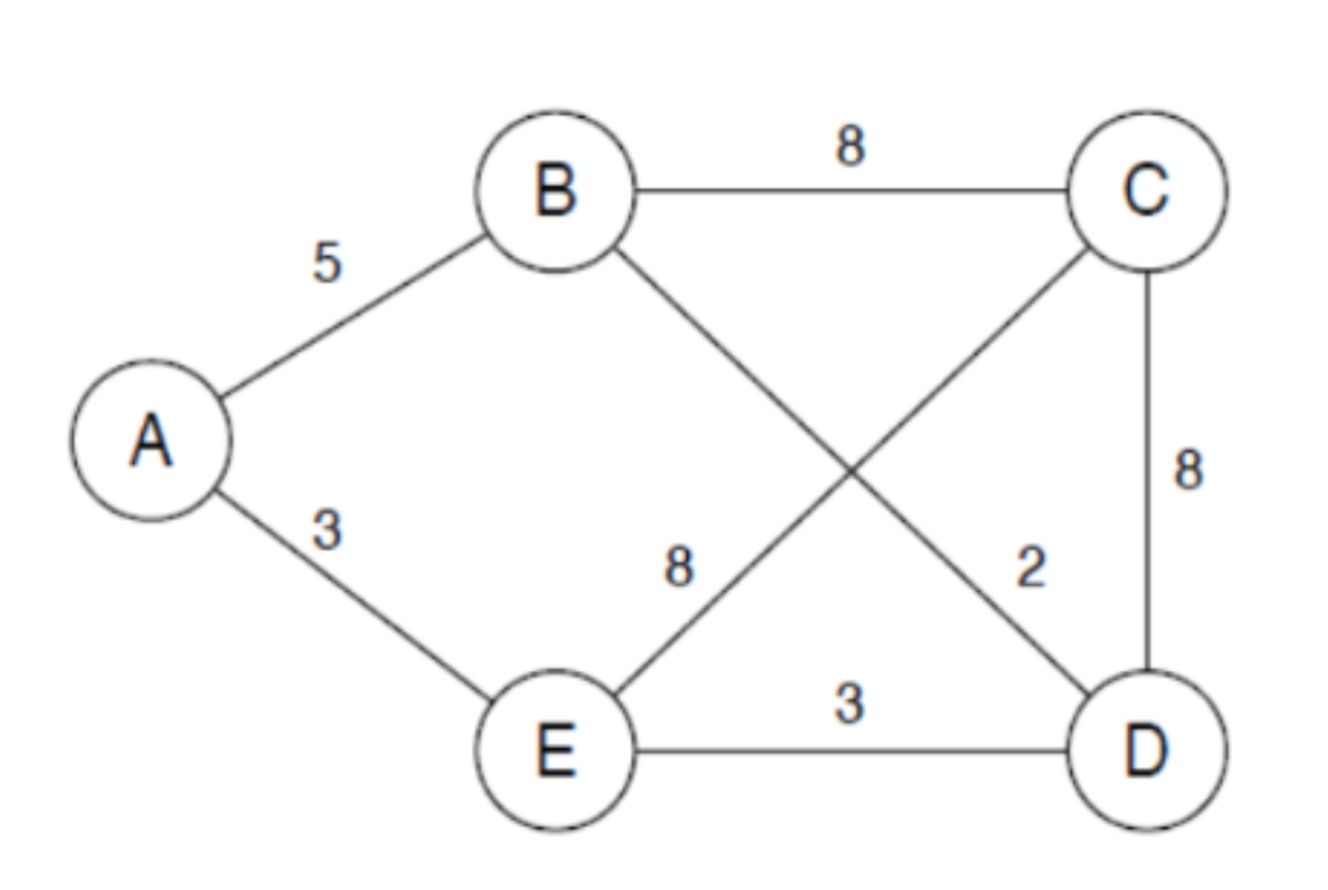
count-to-infinity problem

네트워크에서 노드 링크 사이에 코스트가 매우 크게 변했을 때 node cost table이 무한정 반복적으로 계산하는 문제.

poisoned reverse

z가 y를 거쳐 x로 갈때, 즉 z->x 사이에 y가 끼어있을 경우, y에게 z에서 x로 향하는 거리는 무한대라고 알린다. (무한대라는 말은 ‘너를 거쳐서’ 간다는 표현)